How Do You Determine Which Geometric Series Formula to Use
Aarar2ar3ar4 a a r a r 2 a r 3 a r 4. If youre seeing this message it means were having trouble loading external resources on our website.

Geometric Sequence Formula Chilimath
To find the sum of a finite geometric series we use the formula S_n fracaleft rn 1 rightr 1 for r 1 S_n fracaleft 1 rn right1 r for r 1 Q3.

. An ran1 a n r a n 1. A1 a1r a1r2. If you calculate the same ratio between any two adjacent terms chosen from the sequence be sure to put the later term in the numerator and the earlier term in the denominator then the sequence is a Geometric.
A 8 1 279936 Next simplify the exponent 6 7. If a is 100 and r is 01 you get And if a is 12 and r is also 12 you get the series. The formula of the sum of geometric series is given by.
Sum infty_ n0arnsum infty_ n0frac12left frac23rightn. Find the sum of the first 8 terms of the geometric series if a 1 1 and r 2. Sum of first n terms of a geometric series is given by.
To use the geometric series formula. As the index increases each term will be. 212010 120 210241013 19 2 1 20 10 1 20 2 1024 10 13 19.
Sum of a geometric series. Formula for Finding the Sum of a Geometric Series. Here a is the first term of the series and r is the common ratio.
S n a r n 1 r 1. I can use this to solve for the value of the common ratio r. There are countless plug and chug type exercises.
EXERCISES ON THE GEOMETRIC SERIES. What is the sum of n terms of a Geometric series. That means we can only find the sum for the first n terms.
Put the values in the geometric series formula as per the requirement - the sum of a finite geometric sequence the sum of an infinite geometric series or the n th term of a geometric sequence. We start by using the Arithmetic Series formula to find the sum of various Arithmetic Series and then we will work backwards from our Sum and locate the first term and the common difference. Geometric Series is an old and trusted friend rather than something that first arises as the case p -1of the binomial series 4 p.
Given the great utility of the Geometric Series any exercise that makes it more familiar will be useful. We can use the values of. To find the sum of a finite geometric series use the formula S n a 1 1 r n 1 r r 1 where n is the number of terms a 1 is the first term and r is the common ratio.
By the way the 3 in this example is called the common ratio because the ratio of any term divided by its preceding term equals 3 but it probably makes a lot more sense to think of the 3 as your multiplier. I can also tell that this must be a geometric series because of the form given for each term. That is a 12 a 5 r 7.
Practice your understanding of the geometric series formula. In other words the nth partial sum of any geometric sequence can be calculated using the first term and the common ratio. The two terms for which theyve given me numerical values are 12 5 7 places apart so from the definition of a geometric sequence I know that Id get from the fifth term to the twelfth term by multiplying the fifth term by the common ratio seven times.
The 10th term in the series is given by S 10 a1rn 1r 212010 120 a 1 r n 1 r 2 1 20 10 1 20. Continue this process to ensure the ratio of a term to the preceding term is constant throughout. But the common ratio r is uniquely determined by the series.
We know how to find the sum of the first n terms of a geometric series using the formula Sn a11 rn 1 r. N 0arn n 3rn 1 8 1 16 1 32 1 1 1 are all examples of geometric series the last one doesnt converge. R r and the formula for the sum of a geometric series.
A1rn 1. Up to 10 cash back Finite Geometric Series. What Is r in the Geometric Series Formula.
Before we can learn how to determine the convergence or divergence of a geometric series we have to define a geometric series. Sum infty_ n1ar n-1frac a 1-r. S 8 1 1 2 8 1 2 255.
If so the series is geometric. A 8 279936. So this is a geometric series with common ratio r 2.
Check for the given values a r and n. Compare this ratio with the rest and see if theyre equal. Now that we have the series in the right form we can say.
Given the first several terms of an infinite series determine if the sum of the series exists. Since 1 279936 279936 the 6 t h term in the geometric sequence is 279936. A2 3 2 2 3 4 12.
A3 3 2 3 3 8 24. In the geometric series formula r refers to the. Therefore to test if a sequence of numbers is a Geometric Sequence calculate the ratio of successive terms in various locations within the sequence.
An infinite geometric series is an infinite sum whose first term is a1 and common ratio is r and is written. The convergencedivergence rule for geometric series is a snap. How to tell if a series is geometric.
Rewrite the equation using 279936. For example to calculate the sum of the first 15 terms of the geometric sequence defined by an3n1 use the formula with a19and r3. In your question r 2 3 a 3 n and the number of terms is n 1 you probably messed up in this part.
6 7 6 6 6 6 6 6 6 which equals 279936. Next we will look at the formula for a Finite Geometric. An arn1 a n a r n 1.
Such a geometric sequence also follows the recursive relation. From the given a 2. From here multiply 1 279936 to get the final answer.
For example the first one is a geometric series because the ratio of consecutive terms is ark 1 ark r. N 0 a r n n 0 1 2 2 3 n. N 1 a r n 1 a 1 r.
Find the ratio of the third term to the second term. Its easy to determine whether a given series is geometric or not we simply find the ratio shared between two consecutive terms. Find the ratio of the second term to the first term.
When they are the series is said to be geometric. For every integer n 1. The n n th term of a geometric sequence with initial value a a and common ratio r r is given by.
20481013 19 2048 10 13 19 10778 10 12.

Geometric Series Examples Solutions Videos Worksheets Games Activities

Geometric Series And Geometric Sequences Basic Introduction Youtube
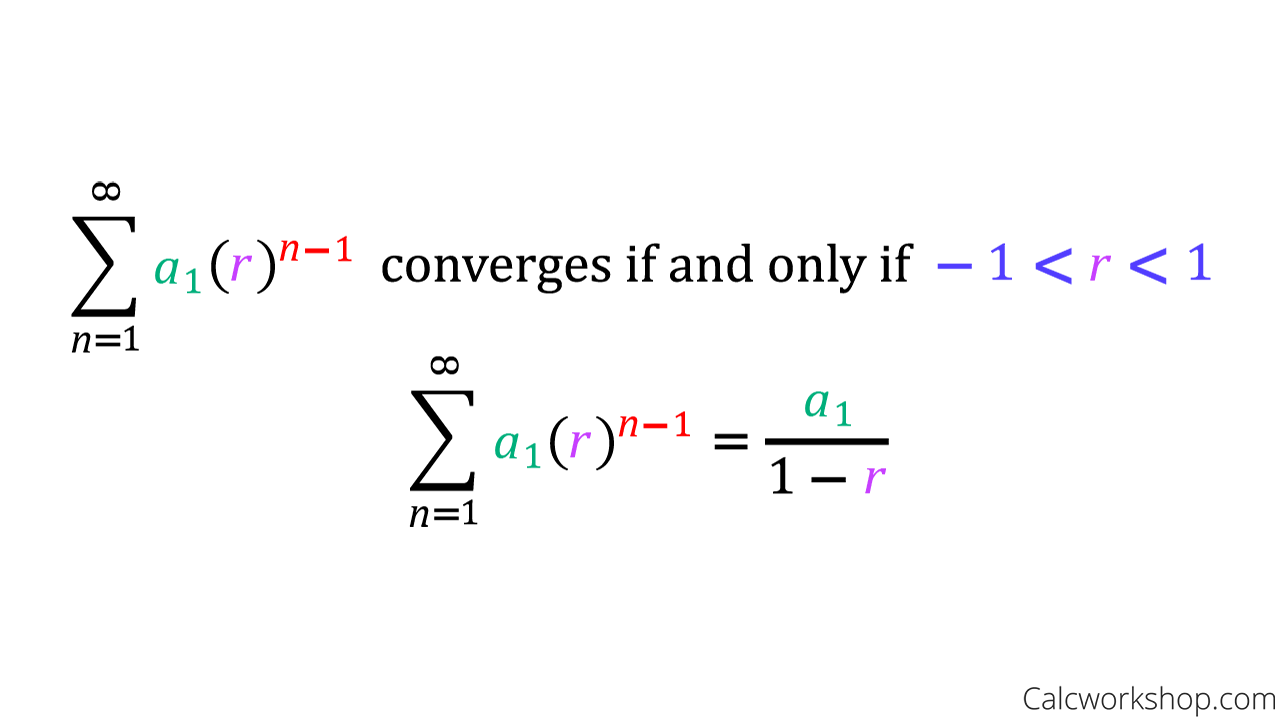
0 Response to "How Do You Determine Which Geometric Series Formula to Use"
Post a Comment